Logisches Quadrat
Das logische
Quadrat ist eine grafische Darstellung der logischen
Relationen zwischen den vier kategorischen Urteilen, die sich aus der
Unterscheidung von zwei Quantitäten des Subjekts (alle, nicht
alle) und zwei Qualitäten des Prädikats (trifft zu,
trifft nicht zu) in einem Satz ergeben. Je nach Kombination ergeben
sich gänzlich oder partiell bestätigende und durch A
und I (aus lat. „affirmo“
–
„ich bejahe“) benannte, sowie gleichfalls
verneinende und durch E und O (aus lateinisch
„nego“
– „ich
verneine“) benannte Urteilstypen. Steht S für
Subjekt und P für Prädikat, so gilt:
- Typ A: „Alle S sind P“ (SaP)
- Typ E: „Alle S sind nicht P“ (SeP)
- Typ I: „Nicht alle S sind nicht P“ (SiP)
- Typ O: „Nicht alle S
sind P“ (SoP)
Daraus ergibt sich das folgende logische Quadrat.
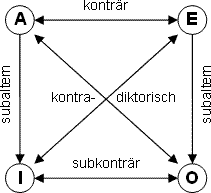
- Konträr:
A ist das genaue Gegenteil von E und somit beides zugleich unmöglich; in Symbolschrift:
¬(A ∧ E) . Möglich ist jedoch, daß beides nicht zutrifft, da zwischen „alle“ und „alle nicht“ Abstufungen vorliegen: ¬A ∧ ¬E. Zusammenfassende Notierung erfolgt mit dem Sheffer-Strich:A | E . - Kontradiktorisch: O ist die Verneinung von A
und widerspricht diesem, so wie I mit E unvereinbar ist. Daher gilt:
O = ¬A bzw. I = ¬E. Durch das Ersetzen ergibt sich jeweils der Satz vom Widerspruch:
¬(A ∧ ¬A) bzw.¬(E ∧ ¬E) . Da die Gegenstücke wegen der wechselseitigen Negation zusammen die gesamte Realität abbilden, ist ihr gleichzeitiges Bestreiten unkorrekt. Die endgültige Notation lautet:A ⊻ O bzw. E ⊻ I, wobei ⊻ „entweder oder“ bzw. Kontravalenz heißt. - Subkonträr: I kann sich nicht nur mit
O partiell decken, sondern beides kann sich ergänzen – der Fall des einschließenden „oder“ bzw. der Disjunktion:
I ∨ O . Da mindesten I oder O gelten muss, ist deren gleichzeitiges Bestreiten unmöglich: ¬(¬I ∧ ¬O) . - Subaltern: A ist hinreichend für I
(bzw. impliziert dieses), so wie E für O. Somit gilt die
Implikation:
A → I ⇔ ¬A ∨ I bzw. E → O ⇔ ¬E ∨ O.
Autor: Dipl. BW (FH) Michael Zabawa
Weiterführende
Literatur

